By: Tao Steven Zheng (鄭濤)

【Problem】

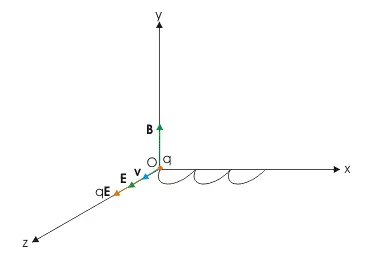
Consider a uniform magnetic field directed in the x-direction, and a uniform electric field directed in the z-direction. A particle with positive charge and mass is released from the origin, and initially at rest. Determine the trajectory of the particle over time.

Hint

【Solution】

The magnetic force is calculated using the cross-product

Subsequently, the Lorentz force, , in vector form is

Divide the mass of the particle on both sides of the equation and let and , then

To solve this system of coupled differential equations, let .

Thus，

Substitute the bottom equation into the derivative of the middle equation to obtain

The above differential equation is non-homogeneous, thus the solution is the sum of the homogeneous solution and particular solution.

(1) Homogeneous solution

The characteristic equation is , where .

The solution is therefore

or

(2) Particular solution

Since is constant, if , then . Then the differential equation?

reduces to

Hence .

Consequently, the solution of the differential equation is

Since the particle is initially released at rest,

To obtain the trajectory,

Since the particle is initially released at the origin,

Replacing and with its original quantities yields

The solution of displacement presents a cycloid trajectory!