Curvilinear Coordinates

2021-09-26 23:28 作者:偏謬Lyx 0人讀過(guò) | 我要投稿

Lamé Coefficients

For any 3D?orthogonal?coordinates? $%5Cmathbf%7Br%7D(q_1%2Cq_2%2Cq_3)$ , the infinitesimal displacement vector can be written as,

$%5Cmathrm%7Bd%7D%5Cmathbf%7Br%7D%3D%5Csum_%7Bi%3D1%7D%5E3%5Cfrac%7B%5Cpartial%5Cmathbf%7Br%7D%7D%7B%5Cpartial%7Bq_i%7D%7D%5C%2C%5Cmathrm%7Bd%7Dq_i$

Define the unit orthogonal basis vectors as,

$%5Cmathbf%7Be%7D_i%20%3D%20%5Cfrac%7B1%7D%7Bh_i%7D%20%5Cfrac%7B%5Cpartial%20%5Cmathbf%7Br%7D%7D%7B%5Cpartial%20q_i%7D$

which? $h_i%20%3D%20%5Cleft%7C%20%5Cfrac%7B%5Cpartial%20%5Cmathbf%7Br%7D%7D%7B%5Cpartial%20q_i%7D%20%5Cright%7C$ ?are called Lamé coefficients.?Following the definition,?we have

$%5Cmathrm%7Bd%7D%5Cmathbf%7Br%7D%3D%5Csum_%7Bi%3D1%7D%5E3h_i%5C%2C%5Cmathrm%7Bd%7Dq_i%5C%2C%5Cmathbf%7Be%7D_i$

The infinitesimal volume is,

$%5Cmathrm%7Bd%7D%5E3%20r%20%3D%20h%20%5C%2C%5Cmathrm%7Bd%7Dq_1%20%5C%2C%5Cmathrm%7Bd%7Dq_2%20%5C%2C%5Cmathrm%7Bd%7Dq_3%2C%20%5Cquad%20(h%20%3D%20h_1%20h_2%20h_3)$

and the infinitesimal area vector in the direction of? $%5Cmathbf%7Be%7D_i$ ?is,

$%5Cmathrm%7Bd%7D%5E2%5Cmathbf%7Br%7D%3D%5Cfrac%7Bh%7D%7Bh_i%7D%5C%2C%5Cmathrm%7Bd%7Dq_j%5C%2C%5Cmathrm%7Bd%7Dq_k%5C%2C%5Cmathbf%7Be%7D_i$

Gradient

For a scalar field? $%5Cvarphi(%5Cmathbf%7Br%7D)$ ,

$%5Cmathrm%7Bd%7D%5Cvarphi%20%3D%20%5Csum_%7Bi%3D1%7D%5E3%20%5Cfrac%7B%5Cpartial%20%5Cvarphi%7D%7B%5Cpartial%20q_i%7D%20%5C%2C%5Cmathrm%7Bd%7Dq_i$

It can also be expressed as,

$%5Cmathrm%7Bd%7D%5Cvarphi%20%3D%20(%5Cnabla%5Cvarphi)%20%5Ccdot%20%5Cmathrm%7Bd%7D%5Cmathbf%7Br%7D%20%3D%20%5Csum_%7Bi%3D1%7D%5E3%20(%5Cnabla%5Cvarphi)_i%20h_i%20%5C%2C%5Cmathrm%7Bd%7Dq_i$

Compare the two expressions, we obtain the components of the gradient,

$(%5Cmathbf%7B%5Cnabla%7D%5Cvarphi)_i%20%3D%20%5Cfrac%7B1%7D%7Bh_i%7D%20%5Cfrac%7B%5Cpartial%20%5Cvarphi%7D%7B%5Cpartial%20q_i%7D$

Therefore,

$%5Cmathbf%7B%5Cnabla%7D%5Cvarphi(%5Cmathbf%7Br%7D)%20%3D%20%5Csum_%7Bi%3D1%7D%5E3%20%5Cfrac%7B1%7D%7Bh_i%7D%20%5Cfrac%7B%5Cpartial%20%5Cvarphi%7D%7B%5Cpartial%20q_i%7D%20%5C%2C%5Cmathbf%7Be%7D_i$

Divergence &?Laplacian

For a vector field,

$%5Cmathbf%7BA%7D(%5Cmathbf%7Br%7D)%20%3D%20%5Csum_%7Bi%3D1%7D%5E3%20A_i(%5Cmathbf%7Br%7D)%20%5C%2C%5Cmathbf%7Be%7D_i$

we have from the calculus that,

$%5Cint_V%20(%5Cnabla%20%5Ccdot%20%5Cmathbf%7BA%7D)%20%5C%2C%5Cmathrm%7Bd%7D%5E3%20r%20%3D%20%5Coint_S%20%5Cmathbf%7BA%7D%20%5Ccdot%20%5Cmathrm%7Bd%7D%5E2%20%5Cmathbf%7Br%7D$

where the volume? $V$ ?is enclosed by the surface? $S$ . Now we shrink? $V$ ?to an infinitesimal cubic volume, such that,

$%5Cbegin%7Bsplit%7D%0A(%5Cnabla%5Ccdot%5Cmathbf%7BA%7D)%5C%2C%5Cmathrm%7Bd%7D%5E%7B3%7Dr%26%3D%20%5Csum_%7Bi%3D1%7D%5E3%5Cleft(%5Cleft.%5Cfrac%7BhA_i%7D%7Bh_i%7D%5Cright%7C_%7Bq_i%2B%5Cmathrm%7Bd%7Dq_i%7D-%5Cleft.%5Cfrac%7BhA_i%7D%7Bh_i%7D%5Cright%7C_%7Bq_i%7D%5Cright)%5C%2C%5Cmathrm%7Bd%7Dq_j%5C%2C%5Cmathrm%7Bd%7Dq_k%5C%5C%0A%25%0A%26%3D%5Csum_%7Bi%3D1%7D%5E3%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%7Bq_i%7D%7D%5C!%5Cleft(%5Cfrac%7BhA_i%7D%7Bh_i%7D%5Cright)%5Cmathrm%7Bd%7Dq_i%5C%2C%5Cmathrm%7Bd%7Dq_j%5C%2C%5Cmathrm%7Bd%7Dq_k%5C%5C%0A%25%0A%26%3D%5Cfrac%7B%5Cmathrm%7Bd%7D%5E%7B3%7Dr%7D%7Bh%7D%5Csum_%7Bi%3D1%7D%5E3%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%7Bq_i%7D%7D%5C!%5Cleft(%5Cfrac%7BhA_i%7D%7Bh_i%7D%5Cright)%0A%5Cend%7Bsplit%7D$

Cancel? $%5Cmathrm%7Bd%7D%5E3%20r$ in both sides to?get the divergence of the field,

$%5Cnabla%5Ccdot%5Cmathbf%7BA%7D(%5Cmathbf%7Br%7D)%3D%5Cfrac1h%5Csum_%7Bi%3D1%7D%5E3%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%7Bq_i%7D%7D%5C!%5Cleft(%5Cfrac%7BhA_i%7D%7Bh_i%7D%5Cright)$

Combine the gradient and the divergence to get Laplacian,

$%5Cbegin%7Bsplit%7D%0A%5Cnabla%5E2%5Cvarphi(%5Cmathbf%7Br%7D)%26%3D%5Cnabla%5Ccdot%5Cnabla%5Cvarphi(%5Cmathbf%7Br%7D)%5C%5C%0A%25%0A%26%3D%5Cfrac1h%5Csum_%7Bi%3D1%7D%5E3%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%7Bq_i%7D%7D%5Cleft%5B%5Cfrac%7Bh%7D%7Bh_i%7D%5Cleft(%5Cnabla%5Cvarphi%5Cright)_i%5Cright%5D%5C%5C%0A%25%0A%26%3D%5Cfrac1h%5Csum_%7Bi%3D1%7D%5E3%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%7Bq_i%7D%7D%5Cleft(%5Cfrac%7Bh%7D%7Bh_i%5E2%7D%5Cfrac%7B%5Cpartial%5Cvarphi%7D%7B%5Cpartial%7Bq_i%7D%7D%5Cright)%0A%5Cend%7Bsplit%7D$

Curl

We have from the calculus that,

$%5Cint_S%20(%5Cnabla%20%5Ctimes%20%5Cmathbf%7BA%7D)%20%5Ccdot%20%5Cmathrm%7Bd%7D%5E2%20%5Cmathbf%7Br%7D%20%3D%20%5Coint_L%20%5Cmathbf%7BA%7D%20%5Ccdot%20%5Cmathrm%7Bd%7D%5Cmathbf%7Br%7D$

where the area? $S$ is?enclosed by the loop? $L$ . Similarly, we shrink? $S$ ?to an infinitesimal area in the direction of? $%5Cmathbf%7Be%7D_1$ , then the loop integral goes along the path as follows,

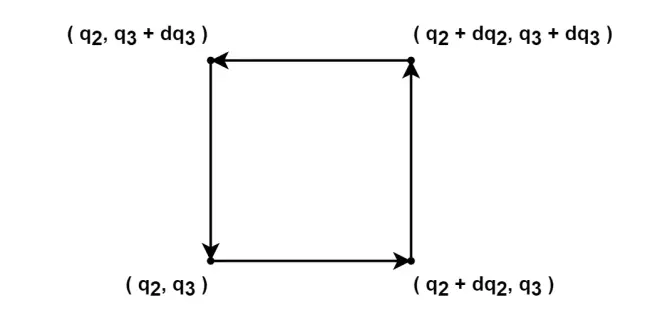
$%5Cbegin%7Bsplit%7D%0A%5Cfrac%7Bh%7D%7Bh_1%7D(%5Cnabla%5Ctimes%5Cmathbf%7BA%7D)_1%5C%2C%5Cmathrm%7Bd%7Dq_2%5C%2C%5Cmathrm%7Bd%7Dq_3%3D%26%5C%2Ch_%7B2%7DA_2%5CBig%7C_%7Bq_3%7D%5Cmathrm%7Bd%7Dq_2-h_%7B2%7DA_2%5CBig%7C_%7Bq_3%2B%5Cmathrm%7Bd%7Dq_3%7D%5Cmathrm%7Bd%7Dq_2%5C%5C%0A%25%0A%26%2Bh_%7B3%7DA_3%5CBig%7C_%7Bq_2%2B%5Cmathrm%7Bd%7Dq_2%7D%5Cmathrm%7Bd%7Dq_3-h_%7B3%7DA_3%5CBig%7C_%7Bq_2%7D%5Cmathrm%7Bd%7Dq_3%5C%5C%0A%25%0A%3D%26%5C%2C%5Cfrac%7B%5Cpartial%5Cleft(h_%7B3%7DA_3%5Cright)%7D%7B%5Cpartial%7Bq_2%7D%7D%5Cmathrm%7Bd%7Dq_2%5C%2C%5Cmathrm%7Bd%7Dq_3-%5Cfrac%7B%5Cpartial%5Cleft(h_%7B2%7DA_2%5Cright)%7D%7B%5Cpartial%7Bq_3%7D%7D%5Cmathrm%7Bd%7Dq_2%5C%2C%5Cmathrm%7Bd%7Dq_3%0A%5Cend%7Bsplit%7D$

Cancel? $%5Cmathrm%7Bd%7D%20q_2%20%5C%2C%5Cmathrm%7Bd%7Dq_3$ ?in both sides to?get one component of the curl,

$(%5Cnabla%20%5Ctimes%20%5Cmathbf%7BA%7D)_1%20%3D%20%5Cfrac%7Bh_1%7D%7Bh%7D%20%5Cleft%5B%20%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20q_2%7D(h_3%20A_3)%20-%20%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20q_3%7D(h_2%20A_2)%20%5Cright%5D$

Switch the index by? $1%20%5Cto%202%20%5Cto%203%20%5Cto%201$ ?to get another two components,

$%5Cbegin%7Balign%7D%0A(%5Cnabla%20%5Ctimes%20%5Cmathbf%7BA%7D)_2%20%26%3D%20%5Cfrac%7Bh_2%7D%7Bh%7D%20%5Cleft%5B%20%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20q_3%7D(h_1%20A_1)%20-%20%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20q_1%7D(h_3%20A_3)%20%5Cright%5D%20%5C%5C%0A(%5Cnabla%20%5Ctimes%20%5Cmathbf%7BA%7D)_3%20%26%3D%20%5Cfrac%7Bh_3%7D%7Bh%7D%20%5Cleft%5B%20%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20q_1%7D(h_2%20A_2)%20-%20%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20q_2%7D(h_1%20A_1)%20%5Cright%5D%0A%5Cend%7Balign%7D$

It can be expressed as a more compact form,

$%5Cnabla%20%5Ctimes%20%5Cmathbf%7BA%7D(%5Cmathbf%7Br%7D)%20%3D%20%5Cfrac%7B1%7D%7Bh%7D%20%5Csum_%7Bi%2Cj%2Ck%7D%20%5Cepsilon%5E%7Bijk%7D%20%5C%2C%5Cmathbf%7Be%7D_i%20h_i%20%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20q_j%7D%5Cleft(h_k%20A_k%5Cright)$

where? $%5Cepsilon%5E%7Bijk%7D$ ?is the Levi-Civita symbol.

Cartesian Coordinates

For Cartesian coordinates? $(x%2Cy%2Cz)$ , it is obvious that,

$h_1%20%3D%20h_2%20%3D%20h_3%20%3D%201$

Gradient

$%5Cnabla%20%5Cvarphi(%5Cmathbf%7Br%7D)%20%3D%20%5Cfrac%7B%5Cpartial%20%5Cvarphi%7D%7B%5Cpartial%20x%7D%20%5C%2C%5Cmathbf%7Be%7D_x%20%2B%20%5Cfrac%7B%5Cpartial%20%5Cvarphi%7D%7B%5Cpartial%20y%7D%20%5C%2C%5Cmathbf%7Be%7D_y%20%2B%20%5Cfrac%7B%5Cpartial%20%5Cvarphi%7D%7B%5Cpartial%20z%7D%20%5C%2C%5Cmathbf%7Be%7D_z$

Divergence

$%5Cnabla%20%5Ccdot%20%5Cmathbf%7BA%7D(%5Cmathbf%7Br%7D)%20%3D%20%5Cfrac%7B%5Cpartial%20A_x%7D%7B%5Cpartial%20x%7D%20%2B%20%5Cfrac%7B%5Cpartial%20A_y%7D%7B%5Cpartial%20y%7D%20%2B%20%5Cfrac%7B%5Cpartial%20A_z%7D%7B%5Cpartial%20z%7D$

Laplacian

$%5Cnabla%5E2%20%5Cvarphi(%5Cmathbf%7Br%7D)%20%3D%20%5Cfrac%7B%5Cpartial%5E2%20%5Cvarphi%7D%7B%5Cpartial%20x%5E2%7D%20%2B%20%5Cfrac%7B%5Cpartial%5E2%20%5Cvarphi%7D%7B%5Cpartial%20y%5E2%7D%20%2B%20%5Cfrac%7B%5Cpartial%5E2%20%5Cvarphi%7D%7B%5Cpartial%20z%5E2%7D%20$

Curl

$%5Cbegin%7Bsplit%7D%0A%5Cnabla%20%5Ctimes%20%5Cmathbf%7BA%7D(%5Cmathbf%7Br%7D)%20%3D%26%5C%2C%20%5Cleft(%20%5Cfrac%7B%5Cpartial%20A_z%7D%7B%5Cpartial%20y%7D%20-%20%5Cfrac%7B%5Cpartial%20A_y%7D%7B%5Cpartial%20z%7D%20%5Cright)%20%5C%2C%5Cmathbf%7Be%7D_x%20%5C%5C%0A%26%2B%20%5Cleft(%20%5Cfrac%7B%5Cpartial%20A_x%7D%7B%5Cpartial%20z%7D%20-%20%5Cfrac%7B%5Cpartial%20A_z%7D%7B%5Cpartial%20x%7D%20%5Cright)%20%5C%2C%5Cmathbf%7Be%7D_y%20%5C%5C%0A%26%2B%20%5Cleft(%20%5Cfrac%7B%5Cpartial%20A_y%7D%7B%5Cpartial%20x%7D%20-%20%5Cfrac%7B%5Cpartial%20A_x%7D%7B%5Cpartial%20y%7D%20%5Cright)%20%5C%2C%5Cmathbf%7Be%7D_z%0A%5Cend%7Bsplit%7D$

Spherical Coordinates

For spherical coordinates? $(r%2C%5Ctheta%2C%5Cphi)$

$%5Cbegin%7Bcases%7D%0A%09x%20%3D%20r%20%5Csin%5Ctheta%20%5Ccos%5Cphi%20%5C%5C%0A%09y%20%3D%20r%20%5Csin%5Ctheta%20%5Csin%5Cphi%20%5C%5C%0A%09z%20%3D%20r%20%5Ccos%5Ctheta%0A%5Cend%7Bcases%7D$

The Lamé coefficients are

$%5Cbegin%7Bcases%7D%0Ah_1%3D1%5C%5C%0Ah_2%3Dr%5C%5C%0Ah_3%3Dr%5Csin%5Ctheta%20%5C%5C%0Ah%3Dr%5E2%5Csin%5Ctheta%0A%5Cend%7Bcases%7D$

Gradient

$%5Cmathbf%7B%5Cnabla%7D%5Cvarphi(%5Cmathbf%7Br%7D)%20%3D%20%5Cfrac%7B%5Cpartial%20%5Cvarphi%7D%7B%5Cpartial%20r%7D%20%5C%2C%5Cmathbf%7Be%7D_r%20%2B%20%5Cfrac%7B1%7D%7Br%7D%20%5Cfrac%7B%5Cpartial%20%5Cvarphi%7D%7B%5Cpartial%20%5Ctheta%7D%20%5C%2C%5Cmathbf%7Be%7D_%5Ctheta%20%2B%20%5Cfrac%7B1%7D%7Br%20%5Csin%5Ctheta%7D%20%5Cfrac%7B%5Cpartial%20%5Cvarphi%7D%7B%5Cpartial%20%5Cphi%7D%20%5C%2C%5Cmathbf%7Be%7D_%5Cphi$

Divergence

$%5Cbegin%7Bsplit%7D%0A%5Cnabla%20%5Ccdot%20%5Cmathbf%7BA%7D(%5Cmathbf%7Br%7D)%20%3D%20%5Cfrac%7B1%7D%7Br%5E2%7D%20%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20r%7D%20%5Cleft(%20r%5E2%20A_r%20%5Cright)%20%26%2B%20%5Cfrac%7B1%7D%7Br%20%5Csin%5Ctheta%7D%20%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20%5Ctheta%7D%20%5Cleft(%20%5Csin%5Ctheta%20A_%5Ctheta%20%5Cright)%20%5C%5C%0A%26%2B%20%5Cfrac%7B1%7D%7Br%20%5Csin%5Ctheta%7D%20%5Cfrac%7B%5Cpartial%20A_%5Cphi%7D%7B%5Cpartial%20%5Cphi%7D%0A%5Cend%7Bsplit%7D$

Laplacian

$%5Cbegin%7Bsplit%7D%0A%5Cnabla%5E2%20%5Cvarphi(%5Cmathbf%7Br%7D)%20%3D%20%5Cfrac%7B1%7D%7Br%5E2%7D%20%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20r%7D%20%5Cleft(%20r%5E2%20%5Cfrac%7B%5Cpartial%20%5Cvarphi%7D%7B%5Cpartial%20r%7D%20%5Cright)%20%26%2B%20%5Cfrac%7B1%7D%7Br%5E2%20%5Csin%5Ctheta%7D%20%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20%5Ctheta%7D%20%5Cleft(%20%5Csin%5Ctheta%20%5Cfrac%7B%5Cpartial%20%5Cvarphi%7D%7B%5Cpartial%20%5Ctheta%7D%20%5Cright)%20%5C%5C%0A%26%2B%20%5Cfrac%7B1%7D%7Br%5E2%20%5Csin%5E2%5Ctheta%7D%20%5Cfrac%7B%5Cpartial%5E2%20%5Cphi%7D%7B%5Cpartial%20%5Cphi%5E2%7D%0A%5Cend%7Bsplit%7D$

Curl

$%5Cbegin%7Bsplit%7D%0A%5Cnabla%20%5Ctimes%20%5Cmathbf%7BA%7D(%5Cmathbf%7Br%7D)%20%3D%26%5C%2C%20%5Cfrac%7B1%7D%7Br%5Csin%5Ctheta%7D%20%5Cleft%5B%20%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%5Ctheta%7D%20(%5Csin%5Ctheta%20A_%5Cphi)%20-%20%5Cfrac%7B%5Cpartial%20A_%5Ctheta%7D%7B%5Cpartial%5Cphi%7D%20%5Cright%5D%20%5C%2C%5Cmathbf%7Be%7D_r%20%5C%5C%0A%26%2B%20%5Cfrac%7B1%7D%7Br%7D%20%5Cleft%5B%20%5Cfrac%7B1%7D%7B%5Csin%5Ctheta%7D%20%5Cfrac%7B%5Cpartial%20A_r%7D%7B%5Cpartial%5Cphi%7D%20-%20%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20r%7D%20(r%20A_%5Cphi)%20%5Cright%5D%20%5C%2C%5Cmathbf%7Be%7D_%5Ctheta%20%5C%5C%0A%26%2B%20%5Cfrac%7B1%7D%7Br%7D%20%5Cleft%5B%20%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20r%7D%20(r%20A_%5Ctheta)%20-%20%5Cfrac%7B%5Cpartial%20A_r%7D%7B%5Cpartial%5Ctheta%7D%20%5Cright%5D%20%5C%2C%5Cmathbf%7Be%7D_%5Cphi%0A%5Cend%7Bsplit%7D$

Cylindrical Coordinates

For spherical coordinates? $(r%2C%5Cphi%2Cz)$

$%5Cbegin%7Bcases%7D%0A%09x%20%3D%20r%20%5Ccos%5Cphi%20%5C%5C%0A%09y%20%3D%20r%20%5Csin%5Cphi%20%5C%5C%0A%09z%20%3D%20z%0A%5Cend%7Bcases%7D$

The Lamé coefficients are

$%5Cbegin%7Bcases%7D%0Ah_1%3D1%5C%5C%0Ah_2%3Dr%5C%5C%0Ah_3%3D1%5C%5C%0Ah%3Dr%0A%5Cend%7Bcases%7D$

Gradient

$%5Cmathbf%7B%5Cnabla%7D%5Cvarphi(%5Cmathbf%7Br%7D)%20%3D%20%5Cfrac%7B%5Cpartial%20%5Cvarphi%7D%7B%5Cpartial%20r%7D%20%5C%2C%5Cmathbf%7Be%7D_r%20%2B%20%5Cfrac%7B1%7D%7Br%7D%20%5Cfrac%7B%5Cpartial%20%5Cvarphi%7D%7B%5Cpartial%20%5Cphi%7D%20%5C%2C%5Cmathbf%7Be%7D_%5Cphi%20%2B%20%5Cfrac%7B%5Cpartial%20%5Cvarphi%7D%7B%5Cpartial%20z%7D%20%5C%2C%5Cmathbf%7Be%7D_z$

Divergence

$%5Cnabla%20%5Ccdot%20%5Cmathbf%7BA%7D(%5Cmathbf%7Br%7D)%20%3D%20%5Cfrac%7B1%7D%7Br%7D%20%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20r%7D%20%5Cleft(%20r%20A_r%20%5Cright)%20%2B%20%5Cfrac%7B1%7D%7Br%7D%20%5Cfrac%7B%5Cpartial%20A_%5Cphi%7D%7B%5Cpartial%20%5Cphi%7D%20%2B%20%5Cfrac%7B%5Cpartial%20A_z%7D%7B%5Cpartial%20z%7D$

Laplacian

$%5Cnabla%5E2%20%5Cvarphi(%5Cmathbf%7Br%7D)%20%3D%20%5Cfrac%7B1%7D%7Br%7D%20%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20r%7D%20%5Cleft(%20r%20%5Cfrac%7B%5Cpartial%20%5Cvarphi%7D%7B%5Cpartial%20r%7D%20%5Cright)%20%2B%20%5Cfrac%7B1%7D%7Br%5E2%7D%20%5Cfrac%7B%5Cpartial%5E2%20%5Cvarphi%7D%7B%5Cpartial%20%5Cphi%5E2%7D%20%2B%20%5Cfrac%7B%5Cpartial%5E2%20%5Cvarphi%7D%7B%5Cpartial%20z%5E2%7D$

Curl

$%5Cbegin%7Bsplit%7D%0A%5Cnabla%20%5Ctimes%20%5Cmathbf%7BA%7D(%5Cmathbf%7Br%7D)%20%3D%26%5C%2C%20%5Cleft(%20%5Cfrac%7B1%7D%7Br%7D%20%5Cfrac%7B%5Cpartial%20A_z%7D%7B%5Cpartial%5Cphi%7D%20-%20%5Cfrac%7B%5Cpartial%20A_%5Cphi%7D%7B%5Cpartial%20z%7D%20%5Cright)%20%5C%2C%5Cmathbf%7Be%7D_r%20%5C%5C%0A%26%2B%20%5Cleft(%20%5Cfrac%7B%5Cpartial%20A_r%7D%7B%5Cpartial%20z%7D%20-%20%5Cfrac%7B%5Cpartial%20A_z%7D%7B%5Cpartial%20r%7D%20%5Cright)%20%5C%2C%5Cmathbf%7Be%7D_%5Cphi%20%5C%5C%0A%26%2B%20%5Cfrac%7B1%7D%7Br%7D%20%5Cleft%5B%20%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20r%7D%20(r%20A_%5Cphi)%20-%20%5Cfrac%7B%5Cpartial%20A_r%7D%7B%5Cpartial%5Cphi%7D%20%5Cright%5D%20%5C%2C%5Cmathbf%7Be%7D_z%0A%5Cend%7Bsplit%7D$

標(biāo)簽：場(chǎng)論 Math 梯度旋度散度拉梅系數(shù)曲線坐標(biāo)

五月天青色头像情侣网名,国产亚洲av片在线观看18女人,黑人巨茎大战俄罗斯美女,扒下她的小内裤打屁股

Curvilinear Coordinates

Lamé Coefficients

Gradient

Divergence &?Laplacian

Curl

Cartesian Coordinates

Spherical Coordinates

Cylindrical Coordinates